최근접 이웃 탐색

알고리즘을 공부하다보면 "최근접 이웃 탐색" 이라는 개념을 마주하게 된다. 이는 보통의 알고리즘의 초반 탐색 부분과 다른 결과를 보여주는데 그 이유는 원하는 값을 찾기보다 단지 가까운 이웃을 리턴하기 때문이다.

따라서 목적성이 다르다. 예를 들면, 우리가 미국에 놀러갔고 지금 내 호텔에서 가까운 커피숍을 찾는다고 해보자. 이 경우 특정 커피숍을 찾는다고 가정할순 없지만(어떤 커피숍이 있는지 정보도 없기 때문), 가장 가까운 커피숍을 찾는 시도는 해볼수 있다.

coffee_maps = [(1, 2), (2, 3), (3, 4), (4, 5)]
here = (4,6)

만약 우리에게 커피숍의 이차원 좌표가 놓여져있는 지도가 있고, 내 위치 좌표가 있다고 해보자. 그렇다면 어떻게 찾아볼수 있을까? 일단 가장 쉽게 우리가 학창시절에 배운 유클리드 거리를 이용해볼수 있다.

dist = math.sqrt(((x1 - x2)^2 + (y1 - y2)^2))

이 유클리드 거리를 기반으로 선형탐색을 하면 쉽게 가까운 커피숍을 찾아볼수 있다.

candidate = coffee_maps[0]
closet = dist(here.x, candidate.x, here.y, candidate.y)
for pos in coffee_maps:
    curr = dist(here.x, pos.x, here.y, pos.y)
    if curr < closet:
        candidate = pos
        closet = curr

return candidate

아주 단순하고 간단하게 가까운 커피숍을 찾을 수 있다. 하지만, 커피숍의 위치가 담긴 지도가 100,000개 혹은 백만개로 더 커진다면 어떨까? 우리는 사실 탐색하지 않아도 커피숍과 나와의 거리를 탐색하게 될수도 있다. 따라서 더 좋은 방법을 고민해보아야 한다.

격자(Grid)

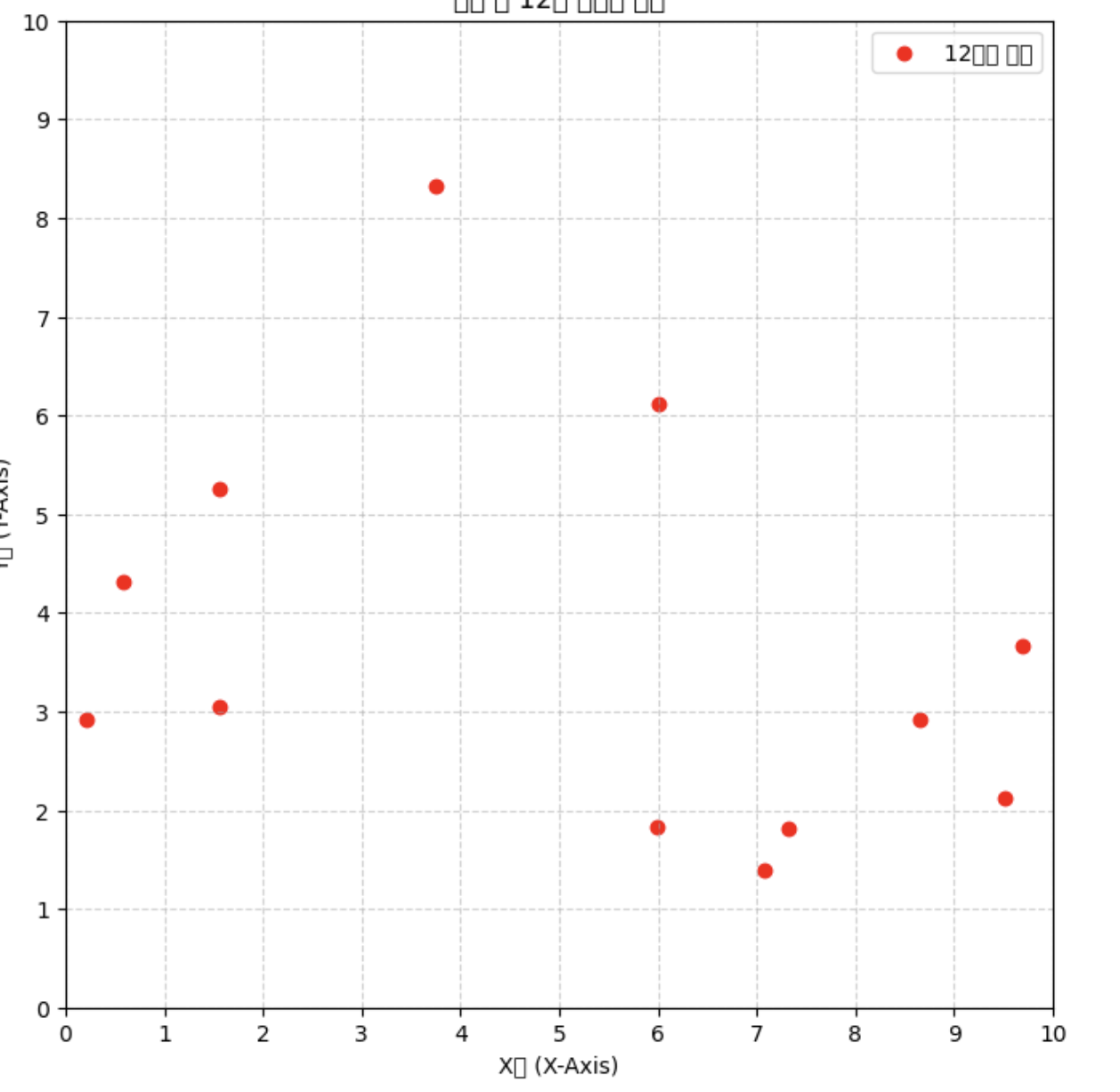
격자는 이러한 고민을 위해 우리가 구해야 하는 거리를 Point 에서 Grid 수준으로 끌어올려 탐색의 가짓수를 줄이는 방법이다. 사진을 보면, 점(7.08, 1.39) 와 점(7.32, 1.82) 는 같은 Grid 안에 있다. 만약 해당 Grid 안에 내가 들어가 있었다면 다른 Point 들은 볼 필요도 없이, 해당 Grid 혹은 인접안 3*3 정도의 Grid 에 속한 Point 들만 확인하면 될것이다.

이제 Grid 에 대한 개념은 이해했으니 Bin 을 어떻게 쉽게 찾을지 생각해보자. 가장 쉬운 방법은 xbin, ybin 과 같은 좌표로 인덱싱 하는 것이다. 즉, (0, 0) 은 첫번째 상자, (0, 1)은 두번째 상자.. 와 같은 방식으로 말이다.

이제 Bin 을 인덱싱하는 방법도 정의했으니 우리가 어떻게 Grid 로 공간을 정의해야 할 것인지 나타내야 한다. 아주 쉽게는 Grid 의 x축의 시작점, 끝점 그리고 y축도 동일하게 시작점, 끝점을 정의해볼수 있다.

type Grid struct {
    x_start float
    x_end float
    y_start float
    y_end float
}

근데 몇개의 Bin 을 우리가 생성할 것인가? X 축의 시작이 (0, 10), y축도 동일하게 (0, 10) 일때 격자를 10개씩 각 축을 기준으로 생성한다고 해보자.

type Grid struct {
    num_x_bins int
    num_y_bins int
    x_start float
    x_end float
    y_start float
    y_end float
}

그렇다면 각 Bin 의 가로와 세로길이는 아래와 같이 정의될 것이다.

x_bin_width := (x_end - x_start) / num_x_bins
y_bin_width := (y_end - y_start) / num_y_bins

이 상태에서 해당 한점 (x,y) 가 어느 Bin 안에 속해야 할지는 어떻게 계산할 수 있을까? X 축을 구하기 위해서는 bin 의 x_width 로 나눠주면 되고, Y 축 또한 y_width 로 나눠주면 된다.

xbin := Floor((x - x_start) / x_bin_width)
ybin := Floor((y - y_start) / y_bin_width)

그렇다면 Bin 내부에서는 점들을 어떻게 관리해야 할까? 여러가지 자료구조가 떠올르지만 정적으로 갯수가 정해지지않았으므로 LinkedList 를 이용해보면 좋을거 같다. (쉽게 구현하려면 언어에서 제공해주는 array 를 써도 좋다)

type GridPoint struct {
    x float
    y float
    next *GridPoint
}

삽입

이제 간단한 수학적인 부분에 대한 정의는 다뤘으므로 값을 넣을때를 한번 생각해보자. 값을 넣을때는 어떻게 넣으면 될까? 일단 이 Point 가 어느격자에 들어가야 하는지 계산해야 한다.

```go=
func (g *Grid) Insert(x float, y float) {
xbin := Floor((x - g.x_start) / g.x_bin_width)
ybin := Floor((y - g.y_start) / g.y_bin_width)

if xbin < 0 || xbin >= g.num_x_bins {
    return false // 혹은 에러 처리
}
if ybin < 0 || ybin >= g.num_y_bins {
    return false // 혹은 에러 처리
}

// 최상단에 배치
next := g.bins[xbin][ybin]
g.bins[xbin][ybin] := &GridPoint(x, y)
g.bins[xbin][ybin].next = next

}

위와 같이 삽입하면 아주 쉽게 원하는 Bin 속에 Point 를 채워 넣을수 있다. 여기까지는 앞에 과정을 이해했다면 아주 쉽게 이해했을거라고 생각한다. 그렇다면 이 Grid 를 이용해서 어떻게 빨리 찾을 수 있을까?

## 탐색

탐색은 간단하게 어디서 찾을 수 있는가 보다는 어떠한 Bin 을 안봐도 되는가로 생각해보면 쉽다. 예를 들면 내 위치가 **(3,5)** 이고 후보인 점은 **(5,6)** 이라고 해보자. 우리는 여기서 내 위치와 후보자의 위치를 기반으로 유클리드 거리 방정식을 통해 거리를 계산해낼 수 있다.

![image.png](https://storage.googleapis.com/roach-wiki/images/06e06da7-8ec0-4e55-b706-1ffc76c1ccc1.webp)

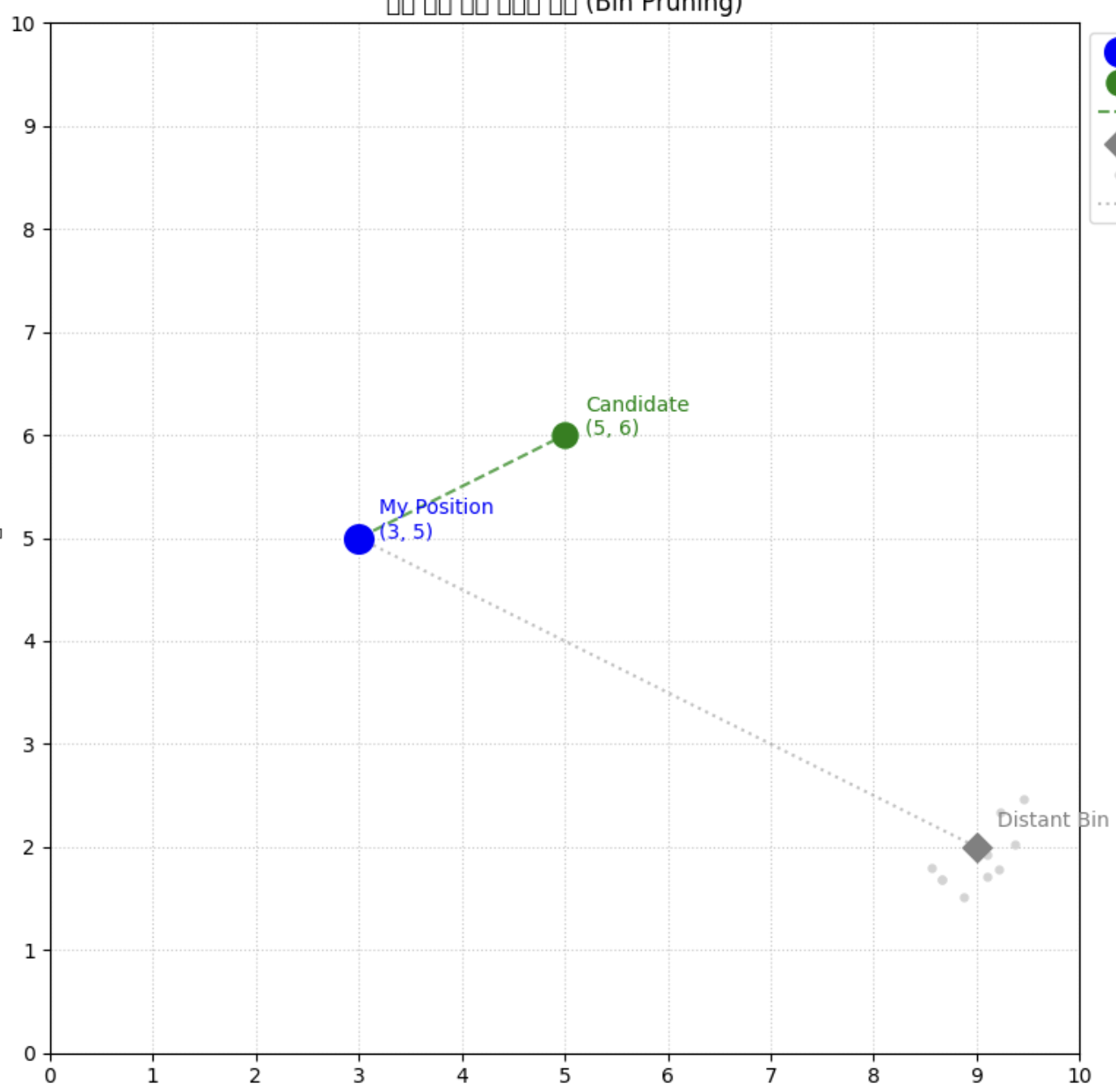
그런데 여기서 나온 거리가 루트 5 일것이다. 그런데 저기 내위치에서 훨씬 먼 Bin(이건 너가 임의로 골라줘) 이 보인다. 해당 Bin 안에 있는 포인트들을 우리가 계산할 필요가 있을까? 아마 없을 것이다. 따라서 우리는 Bin 안의 모든 Point 와의 거리보다 **임의의 Bin 과 내 위치간의 거리를 구해서 현재 후보자와의 거리보다 짧은 경우에만 계산을 진행**하면 된다.

여기서 조금 더 수학적으로 접근해보자면 결국 bin 과 나와의 거리를 구할때 이용할 수 있는 점은 무조건 bin 의 경계에 있을 것이다. bin 의 경계의 점들을 무한할것이므로 특정할수 없으니 각 축의 최솟값과 최댓값을 이용해 거리를 측정해보자.

특정 bin 의 `xmin or ymin` 을 구하려면 bin 의 width 와 인덱스를 곱해주면 된다. 

```python
xmin = x_start + xbin * x_bin_width
ymin = y_start + ybin * y_bin_width

그렇다면 xmax or ymax 는 어떻게 구할까? 이건 사실 다음 bin 의 최솟값과 같을 것이므로 +1 만 해주면 된다.

xmin = x_start + (xbin + 1) * x_bin_width
ymin = y_start + (ybin + 1) * y_bin_width

이걸 이용해 나의 위치 (x, y) 에서 임의의 Bin 과의 거리를 최소거리를 계산해본다면 아래와 같을 것이다.

x_dist = Inf
y_dist = Inf

if x < x_min:
    x_dist = x_min - x
elif x_min <= x <= x_max:
    x_dist = 0
else:
    x_dist x - x_max

if y < y_min:
    y_dist = y_min - y
elif y_min <= y <= y_max:
    y_dist = 0
else:
    y_dist = y - y_max

이걸 Go 코드로 작성해보면 아래와 같이 작성해볼 수 있다.

func (g *Grid) MinDistToBind(xbin int, ybin int, x float64, y float64) float64 {
    // 잘못된 상자인지 아닌지 체크
    if xbin < 0 || xbin >= g.num_x_bins {
        return math.Inf(1)
    }

    if ybin < 0 || ybin >= g.num_y_bins {
        return math.Inf(1)
    }

    x_min := g.x_start + float64(xbin)*g.x_bin_width
    x_max := g.x_start + float64(xbin+1)*g.x_bin_width
    x_dist := float64(0)
    if x < x_min {
        x_dist = x_min - x
    }
    if x > x_max {
        x_dist = x - x_max
    }

    y_min := g.y_start + float64(ybin)*g.y_bin_width
    y_max := g.y_start + float64(ybin+1)*g.y_bin_width
    y_dist := float64(0)
    if y < y_min {
        y_dist = y_min - y
    }
    if y > y_max {
        y_dist = y - y_max
    }

    return math.Sqrt(x_dist*x_dist + y_dist*y_dist)
}

이제 나의 위치로 부터 Bin 까지 최소거리를 구하는 함수는 완성됬으므로 이걸 이용해서 선형탐색을 하며 탐색해야할 Bin 을 가지치기해보자

가지치기

일단 선형탐색으로 가지치기를 어떻게 진행할지 생각해보면 내 위치와 모든 bin 들과의 거리를 계산해보면서 만약 그게 지금까지 구한 최소 거리(best_dist) 보다 작은 경우에만 Bin 내부의 점(GridPoint)들을 순회하며 최소거리를 업데이트 하는 방식이다.

코드로 작성해보면 아주 쉽게 작성할 수 있다.

func (g *Grid) LinearScan(x float64, y float64) *GridPoint {
    best_dist := math.Inf(1)
    var best_candidate *GridPoint
    xbin := 0
    for xbin < g.num_x_bins {
        ybin := 0
        for ybin < g.num_y_bins {
            if g.MinDistToBind(xbin, ybin, x, y) < best_dist {
                current := g.bins[xbin][ybin]
                for current != nil {
                    dist := euclidean_dist(x, y, current.x, current.y)
                    if dist < best_dist {
                        best_dist = dist
                        best_candidate = current
                    }
                    current = current.next
                }
            }
            ybin++
        }
        xbin++
    }
    return best_candidate
}

정리

처음에는 모든 점과의 거리를 계산해야 했지만 격자(Grid) 라는 개념을 도입하고 나서부터는 우리가 봐야할 범위를 가지치기 함으로써 탐색횟수를 줄일 수 있었다. 직관적으로 생각해보면 쉽지만 막상 코드로 이를 작성해보면 구현이 쉽지는 않다는 걸 느낄 수 있다.

다만 지금의 방식도 합리적인 방식은 아니다. 예를 들면, 아래와 같은 생각이 들수도 있다. "이미 내 위치가 특정된 경우에는 사실 내 위치 주변의 3*3 칸만 확인해도 되지 않을까?" 이런 생각들은 충분히 합리적이다. 만약 없으면 그 주변 격자로 BFS 를 진행하면 되기 때문이다. 다음 포스팅에서는 이 탐색 알고리즘을 최소화 하는 포스팅을 적어보려고 한다.

책 추천

이 책은 "읽고 나면 진짜 쉬워지는 자료 구조" 라는 책이다. 개인적으로 특정언어에 조금 더 익숙해지고 싶을때 한번 씩 이책을 읽어보면서 구현해보는걸 추천한다. 꽤나 언어를 숙달시키는데 꽤 도움도 되고, 자료구조를 짜임새 있게 배울 수 있어서 각 자료구조가 어떠한 이유로 탄생했는지 직접 실습해보며 느낄수 있다.